줌달의 일반화학 10판 정리
흐름 check
-물질과 파동은 사실 하나였다
-이를 기반으로 원자 모형(오비탈)을 세웠다
-오비탈에 대해 알아보자
-오비탈로 설명되는 원자의 주기적 성질에 대해 알아보자
-물질과 파동은 하나이다-
전자기 복사 & 파동 성질
전자기 복사
에너지가 공간을 이동하는 방법 (열을 전달하는 방법 중 하나. 0K 이상의 모든 물체는 전자기복사로 에너지 방출 가능)
다양한 형태(태양광, 난로의 열, X선... 즉 감마 X 자외선 어쩌) 그러나 같은 형태의 파동 성질, 진공 중 빛의 속도 가짐

에너지가 전자기복사를 통해 열로 전달, 분자는 열에너지를 흡수해 활발한 운동, 충돌하며 온도를 높임
파동의 3가지 성질
λv=c (2.9979*10^8m/s)
1) 파장(λ): 골과 골 사이 거리
2) 진동수(ν): 공간의 주어진 점을 1초 동안 통과하는 파동의 수
3) 속도(c): 모든 전자기복사는 진공에서 빛의 속도로 진행 (헤르츠=사이클 수/초)

파장이 짧으면 진동수는 크다(반비례)

즉 레이어를 씌운 것처럼.. 한 점을 찍으면 그 점은 가로로 동일한 속도(빛의 속도)로 움직일거고..(근데 이렇게 표현해도 되나?? 제자리에 있다느니 어쩌구 한 것 같은데..) 파장(파장)이 짧으면 같은 가로거리를 이동해도 여러 파장을 거칠거고(진동수 큼)

물질의 성질
물질(입자, 질량과 위치를 가짐)과 에너지(파동, 연속적)은 별개가 아니다
에너지는 물질의 한 형태이다
*빛의 이중성 : 전자기 복사선이 입자의 성질도 보인다 - Plank 상수, Einstein의 광전 효과
*물질도 파동의 성질을 가진다 - de Brogile의 식, 회절
Plank 상수
백열상태로 가열된 고체로부터 방출되는 복사선 연구
→ hv의 정수배에 해당하는 에너지만 흡수/방출 (∆E = nhv)
**h는 플랑크상수 (h=6.626 x 10-34J·s), v는 진동수
→에너지는 양자(hv 크기의 에너지 꾸러미)화되어 있음, 즉 입자와 같음

Einstein의 광전 효과
빛을 금속 표면에 쪼이면 전자가 방출되는 것을 실험
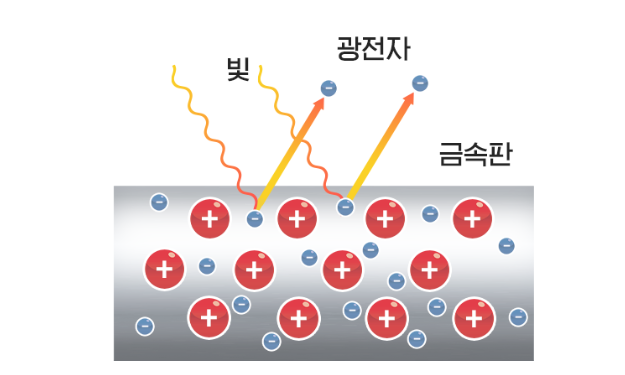
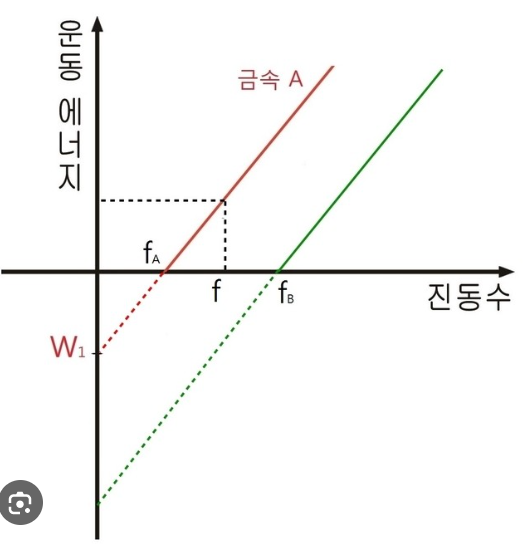

1) 빛의 세기 무관하게 문턱 진동수(금속따라 특정값)를 넘어야 전자가 방출
2) 방출되는 전자의 운동 에너지는 빛의 진동수에 일차 함수로 증가
3) 방출되는 전자의 수는 빛의 세기에 비례
문턱 진동수 E0=hv0
전자의 운동에너지 KE전자=hv-hv0=mv^2/2
전자기 복사는 광자(photon)라는 입자의 흐름이다
광자 하나의 에너지는 hv이다(즉 진동수에 비례) E광자=hv=hc/λ ***플랑크랑도 일치!
특수 상대성 이론에서 E=mc^2, 즉 에너지도 질량을 가진다
광자도 질량을 가진다(입자의 성질) m광자=E/c^2=(hc/λ)/c^2=h/λc

de Broglie의 식
빛의 이중성(특히 전자기 복사 질량 m광자=h/λc)에 주목하고, 물질로 확장함
속도가 v인 입자의 파장에 대한 식. 입자도 파장을 가진다!
m=h/λv → λ=h/mv


m이 큰 보통의 물질은 파장이 너무 짧아 입자의 성질이 주될 뿐
광자처럼 작은 물질은 파동의 성질이 주될 뿐
전자처럼 중간 질량은 입자성질, 파동성질 모두 드러난다
전자의 회절 무늬
빛의 보강/상쇄 간섭으로 인한 회절 현상이 전자에서도 나타남
산란 점 간격이, 파동의 파장과 같을 때 나타나는 현상
→ 전자의 파동성
-원자의 모형-
Bohr 모형
수소의 원자 스펙트럼
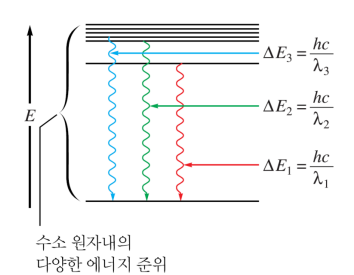
고에너지 수소 원자가 방출하는 빛의 스펙트럼 - 특정 파장에 해당하는 선만 나타남(선 스펙트럼)
수소 원자는 특정 에너지 상태만 허용된다 (양자화) → 그 특정 에너지 값 차이 만큼의 특정 파장 빛만 방출한다
플랑크 식이 적용됨(∆E = hv = hc/λ)
보어의 수소 원자 양자 모형
'수소 원자 전자가, 핵을 따라 어떤 허용된 반지름의 원형궤도만 따라 움직인다' 고 가정
***현대 이론에 따르면 진짜로 전자들이 특정 원형 궤도를 도는게 아니다***
그러나 선 스펙트럼과 잘 일치함
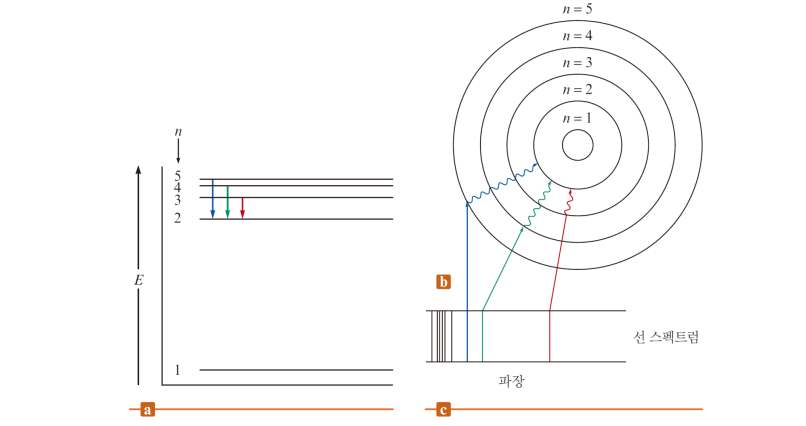
-에너지가 양자화되어 있다
-핵에 가까워질수록 안정하다 (부호가 -인 이유)
★보어 모형에 따른 수소 원자 전자의 허용된 에너지 준위

★보어 모형에 따른 방출되는 빛(광자)의 에너지, 파장
-플랑크 상수 활용


원자의 양자 역학적 모형 (오비탈)
-Heisenberg, de Broglie, Schrodinger의 파동 역학(양자 역학)
슈뢰딩거 방정식
전자를 파동(정류파)으로 보고 원자 구조를 밝히고자 함
→ 전자에게 허용되는 에너지, 공간 분포에 대한 파동함수(오비탈)

*정류파

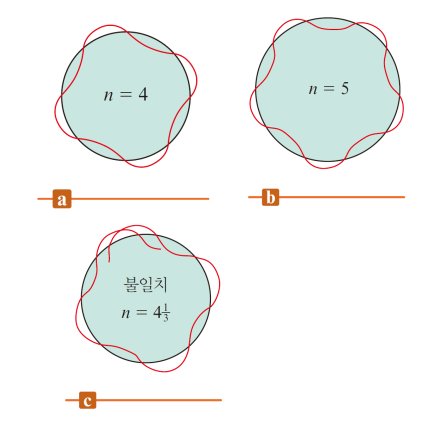
양 끝이 고정된 파동(*node)
파동은 이동하는게 아니라 그 자리에 고정 → 파동의 반파장의 정수배로 딱 떨어져야 허용된 진동
즉 허용되는 파동이 제한됨
Heinsenberg의 불확정성 원리
주어진 순간에 입자의 위치와 운동량(에너지)을 동시에 측정하는 데에는 한계가 있다

질량이 크면 오차가 작아서 괜찮은데..
전자처럼 질량이 작으면(우변으로 넘겨보삼), 위치와 운동량 모두를 알기 더 어려움
그래서 전자의 위치는 영역별 확률을 계산하는 것이 최선이다
(보어처럼 궤도따라 움직이는게 아님)
파동함수 오비탈의 물리적 의미
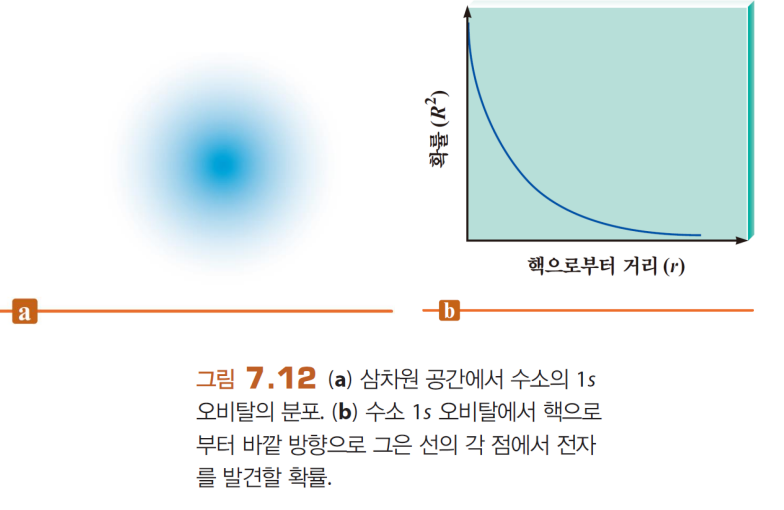
파동함수의 제곱(확률분포)은 특정 점에서 전자를 발견할 확률
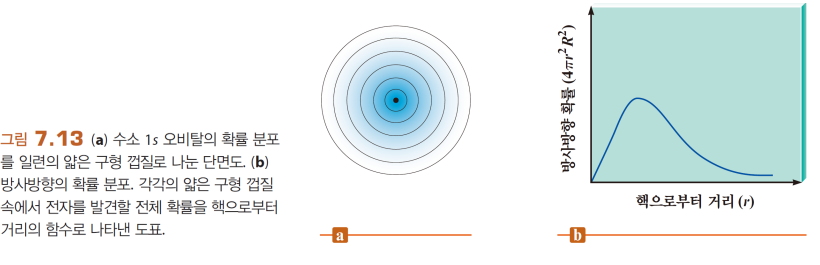
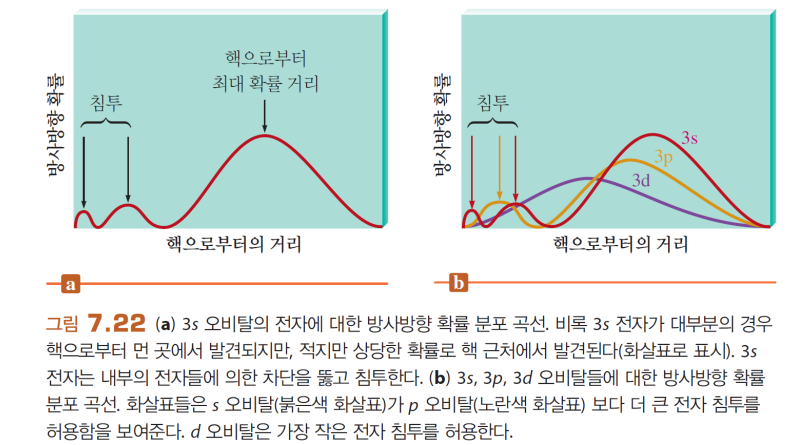
*방사 확률 분포
한 점(왼쪽)에서의 확률만 보면, 핵에서 가까울수록 확률이 크지만
거리(r)의 관점에서 보면, 멀수록 부피가 커지니 최대인 거리가 존재함
→ 오비탈은 90% 발견할 확률을 포함하는 표면이다. 그 표면이 오비탈의 크기!
어떠한 원소에 대해서, 이와 같은 파동함수를 여러 개 얻을 수 있다
따라서 다양한 오비탈을 가지는 것!
-오비탈-
오비탈의 양자수
어떠한 원소에 대해서, 이와 같은 파동함수를 여러 개 얻을 수 있다
따라서 다양한 오비탈을 가지는 것!
그리고 이 오비탈들은 여러 성질을 가진다
그 성질을 나타내는 것이 양자수이다!
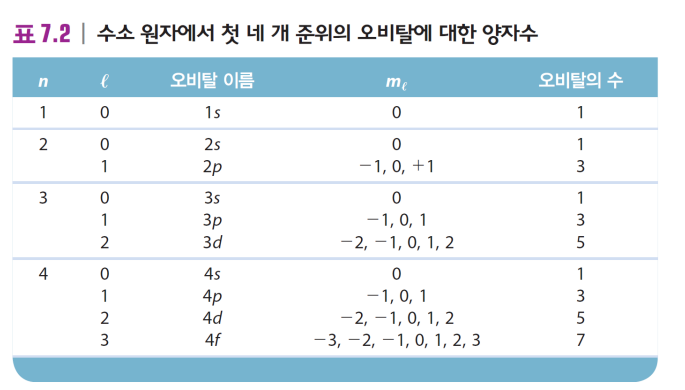
| 주양자수 (n=1, 2, 3...) | 각 운동량 양자수 (l=0, 1, 2.. n-1) | 자기 양자수 (ml= -l, .., 0, ... +l) | 전자 스핀 양자수 (ms= -1/2, +1/2) |
| -오비탈의 크기와 에너지를 나타냄 (숫자가 클수록 둘 다 큼) | -오비탈의 모양을 나타냄 -s, p, d, f, g  |
-오비탈의 상대적 배향 // 개수도 얘로 세면 됨 | -전자의 두 가지 배향의 자기 운동량 -회전하는 전하가 가지는 운동량임 ***Pauli 배타 원리에 의해, 같은 오비탈의 전자는 무 조 건 서로 다른 ms값을 가짐*** |
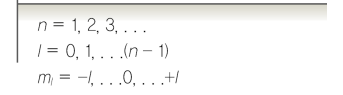
오비탈의 모양과 에너지
모양 (s, p, d, f)
 |
  |
 |
 |
마디(node) : 오비탈이 0의 확률을 갖는 공간, n이 클수록 많아짐
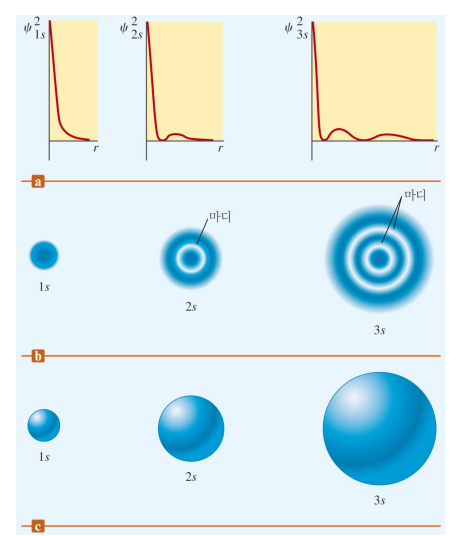
오비탈의 위상(p) : p오비탈부터는 사인파처럼 위상을 가짐. 각 로브가 다른 부호의 위상
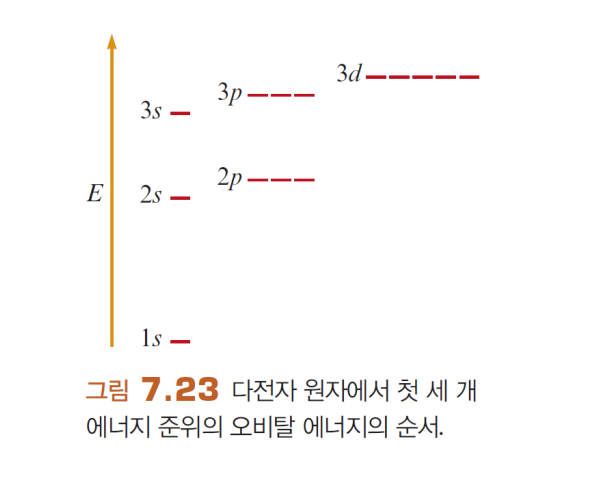
오비탈의 에너지
| 수소 원자 - 축퇴되었다 | 다전자 원자 - 차폐되었다 |
| n값이 결정. s, p, d, f 등 모양은 무관함 -1s가 바닥상태  |
다양한 요소들이 작용함 같은 주양자 준위여도 다른 에너지를 가짐   |
다전자 원자의 에너지
전자의 운동 E + 전자 간 반발에 의한 PE + 핵과 전자 간 인력에 의한 PE
*전자 상관 문제: 전자의 경로가 알려지지 않아, 전자 간 반발 계산 불가
→ 반발력+인력 알짜 전하장 근사법 이용 (전자들의 반발력으로 인해, 핵 전하로부터 차폐되었다)
→ 모양적으로 수소형 궤도함수를 얻을 수 있음. 단 크기와 에너지는 다름
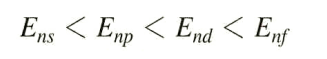
침투 효과
같은 n의 궤도함수를 보면,
s-p-d-f 순으로 최대확률은 멀지만, 핵과 가까운 작은 봉우리가 존재함. 즉 더 침투함.
따라서 더 강하게 핵에 끌려 낮은 에너지 상태를 가지게 됨
→ (1)동일n에서 s<p<d<f (2) nd보다 (n+1)s가 먼저인 이유
-주기율표와 전자배열-
멘델레예프가 원자량으로..
전자배열
3가지 배열 규칙
| 1) 파울리 배타 원리 (절대적!!) | 2) 쌓음 원리 (바닥) | 3) Hund의 규칙 (바닥) |
| 한 원자에서 어떠한 두 원자도 같은 4개의 양자수를 가질 수 없다 즉, 한 궤도함수의 두 전자는 서로 반대의 스핀 |
낮은 에너지 준위부터 |
같은 에너지일 때 홀전자 수가 최대인 배치로 |
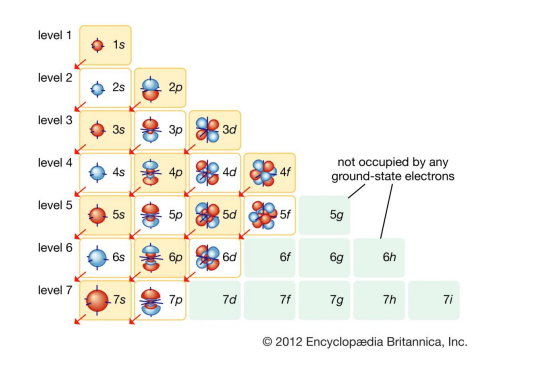
에너지 준위 순서
*(n+1)s → nd
침투효과에 의해, (n+1)s가 침투 정도가 너무 커서 nd보다 에너지가 낮아짐
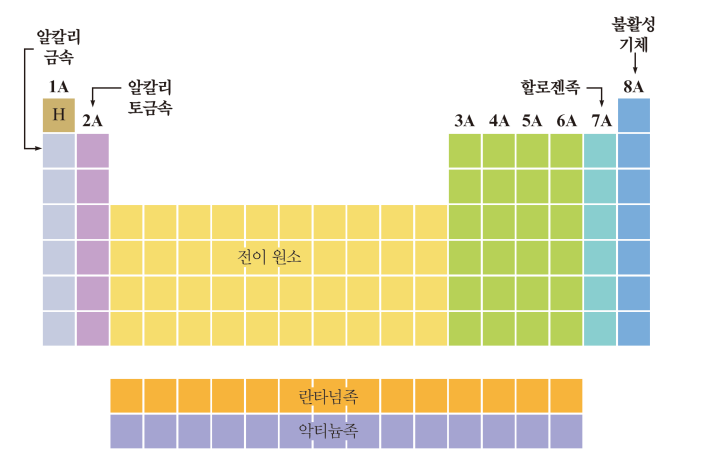
*1A~8A를 주족 또는 전형원소라고 한다
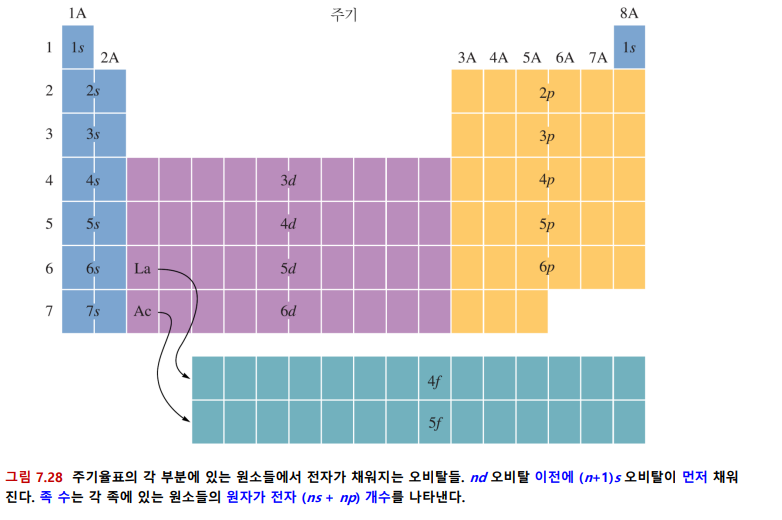
*란타넘 족: 란타넘( [Xe]6s25d1 ) 이후 14개의 원소들
4f보다 5d에 먼저 전자가 1개 채워진다
7개의 4f 오비탈들이 채워진다
4f와 5d의 에너지가 너무 비슷해서이다
*악티늄 족: 악티늄 ( [Rn]7s26d1 ) 이후 14개 원소들
5f보다 6d에 먼저 전자가 1개 채워진다
7개의 5f 오비탈들이 채워진다
5f와 6d의 에너지가 너무 비슷해서이다
예외 사항
Cr: [Ar]4s1 3d5
Cu: [Ar} 4s1 3d10
원자가 전자
가장 바깥 주양자 준위에 위치한 전자
그 반대로 내부 전자는 핵심부 전자라고 한다
같은 족이면 동일한 원자가 전자 → 유사한 화학적 성질
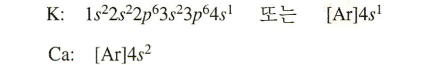
-원자의 주기성-
원자 성질의 경향성
| 이온화 에너지 (l) 바닥 상태에서 전자 1개 제거할 때 필요한 에너지. (1,2,..n차 이온화 에너지) 즉 바닥상태에서 바뀌는거니 에너지를 필요로 하는!! |
전자 친화도 기체 상태 원자에 전자 하나를 더하는데 관련된 에너지 변화 발열이거나 흡열이거나 둘 다 있음 |
원자 반지름 이원자 분자 or 공유 결합 or 금속 결정 |
오른/위로 갈수록 셈   *불연속적인 구간(더 떼기 쉬워짐) -꽉 찬 2s오비탈이 2p 전자 핵전하 가림 -전자 짝이 있어서 반발력 n차에서 비교 *n차: 갈수록 이온화 에너지가 커짐 -전하가 더 양전하가 되어서 전자를 당김 -가령 s가 p보다 안정하기 때문 *급격하게 이온화 에너지가 커지는 구간 -n이 작아져서(더 강한 핵심부 전자) |
오른으로 갈수록 음의 값 (더 전자 잘 받음)  *예외 N- N의 2p3는 이미 전자가 있는 오비탈에 들어가야 해서 반발력 → 불안정 O부터는 핵전하가 반발력 커버쳐줌 |
왼/아래로 갈수록 커짐 -오른은 유효 핵전하 증가해서 작아짐 -아래로 가면 주양자수 증가해서 오비탈 커짐  동일 전자수일 때는, 핵전하가 작아야 큼 |
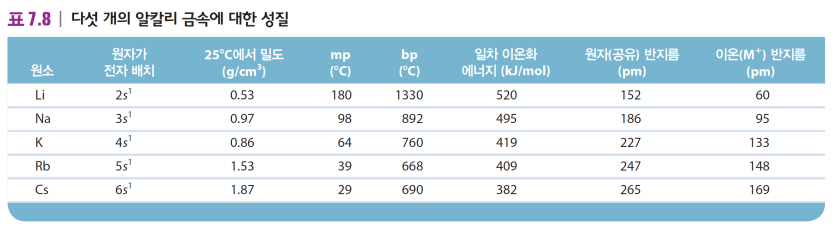
알칼리 금속(1A족)의 성질
큰 화학적 반응성 (낮은 이온화 에너지 → 이온성 고체 형성)
아래로 갈수록 밀도 증가, 환원력 강해짐
'일반화학 > 일반화학 개념정리' 카테고리의 다른 글
| <일반 화학> 8장 후반~9장- 공유 결합: 오비탈 (1) | 2023.05.19 |
|---|---|
| <일반 화학> 8장- 결합: 일반 개념 -1 (1) | 2023.05.18 |
| <일반 화학> 6장- 열역학 (0) | 2023.05.09 |
| <일반 화학> 5장- 기체 (0) | 2023.05.08 |
| <일반 화학> 4장- 화학반응의 종류와 용액의 화학량 (0) | 2023.05.08 |




댓글