줌달의 일반화학 10판 정리
12장. 화학 반응 속도론
- 화학반응의 3요소: 화학량론 + 열역학(자발성) + 반응 속도

- 반응 속도
(1) 반응 속도의 개념과 특성
(2) 반응 속도 법칙 - 미분(초기농도-초기속도) 적분(시간-농도)
(3) 반응 메커니즘 - 단일단계반응, 속도결정단계
(4) 반응 모형 - 온도, 활성화E, 배향
반응 속도란?
정의
속도=Δ[A]/Δt mol/(L*s)
단위 시간당 반응물/생성물의 농도 변화

1. 반응 속도 구하기 - 평균 반응 속도: 시간과 농도
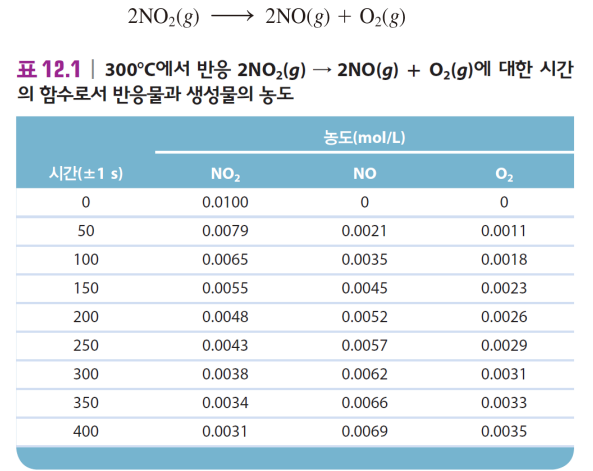
예를 들어, 50초 동안 평균 반응속도는
NO2 기준: -(0.0079-0.0100)mol/L / 50.s = 4.2*10^(-5) mol/(L*s)
2. 반응 속도 구하기 - 순간 속도: 시간 농도 그래프의 접선의 기울기
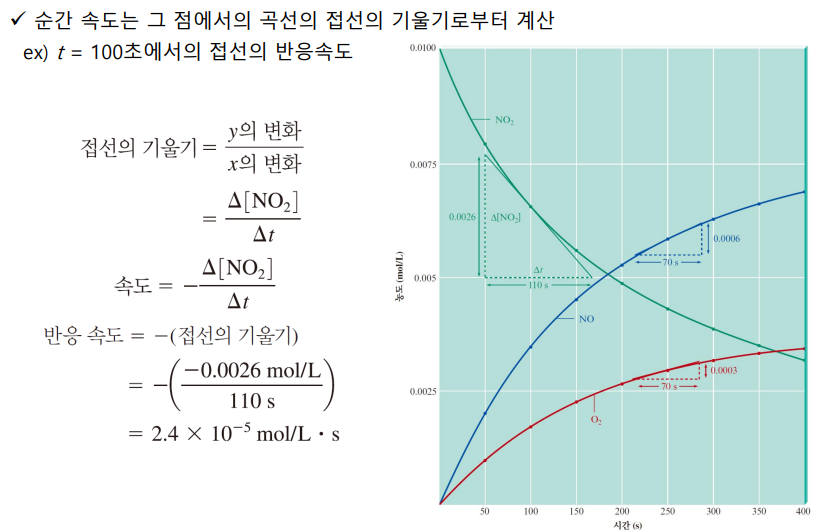
주의사항
*농도는 몰 농도(mol/L)
*항상 양수로 정의: -Δ[반응물]/Δt Δ[생성물]/Δt
*시간에 따라 속도는 감소함: 시간 흐름→ 반응물 농도 적어짐→ 속도 느려짐
*반응식 계수에 의존적: 비례함, 기준을 명확히 해야 함
<시간에 따른 속도 감소>
순간속도(접선의 기울기)는 계속해 감소한다
반응물의 농도가 감소하기 때문이다
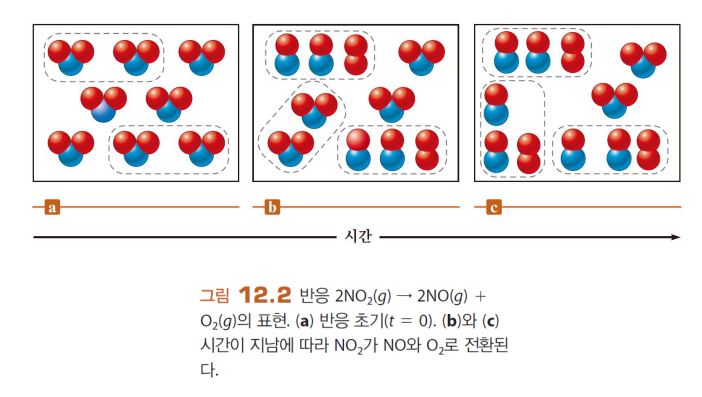
<반응식 계수에 비례>
같은 반응식이라면, 반응식 계수에 비례해 속도가 측정된다
따라서 무엇을 기준으로 잡을 것인지 명확히 해야 한다
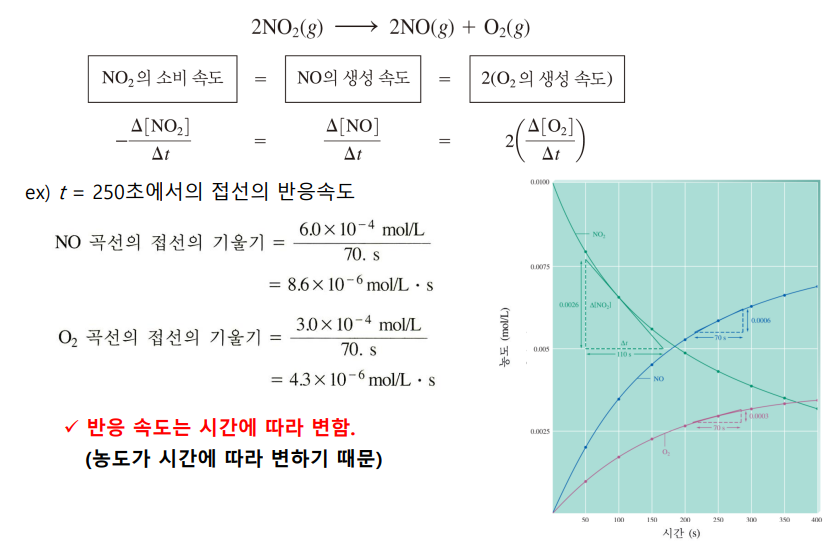
속도법칙: 미분속도법칙, 적분속도법칙
*반응의 가역성과 초기속도법
-역반응을 무시하기 위해 초기 속도법을 이용
대부분 화학반응은 가역적, 즉 생성물이 충분히 생성되면 역반응이 진행된다
이 때 Δ[A]는 정반응과 역반응의 속도 차이로 결정되어 복잡해진다
그러나 반응 초기(생성물 생성 전)에는 속도가 반응물의 (초기)농도에만 의존해 간단하다 ▷ 초기 속도법, 속도 법칙
v=k[A]^n (***k와 n은 실험적으로 결정, 반응식과는 무관) ▷ 속도 법칙

미분 속도법칙 & 적분 속도법칙
| 미분 속도 법칙 반응속도=f(농도) |
적분 속도 법칙 농도=f(시간) |
|
| 식 | v = k[A]^n [B]^m ex. 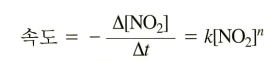 |
0차 [A]=-kt + [A]0 1차 ln[A] = -kt + ln[A]0 2차 1/[A] = kt + 1/[A]0 |
| 유형 =반응식 =차수 결정 |
*초기속도법(초기농도-초기속도 그래프) 1. 초기농도 변화에 따른 속도 변화가 몇제곱인지 구한다 2. (초기농도, 초기속도) 대입해 k를 구한다 식 완성 |
*시간-농도 그래프 1. ln[A], 1/[A], [A] 중 1차적인 것을 고른다 2. 차수를 결정하고, 기울기로 k를 구한다 식 완성 그 외 반감기 구하기, 농도 예측하기 |
-둘은 하나를 알면 다른 하나를 아는 관계이다
-따라서 둘 중 아무 거나 편한 걸로 구하면 된다
-농도-반응속도 측정이 쉬우면 미분, 시간-농도 측정이 쉬우면 적분
-속도법칙을 구하는 이유로, 반응의 메커니즘을 추측할 수 있게 된다
(미분)속도 법칙 : 반응 속도-초기 농도 관계
*정의
v=k[A]^n [B]^m 즉, 이 식이 Δ[A]/Δt와 동일
k는 속도 상수 단위는 반응 차수마다 다름
n, m은 반응 차수 / n+m은 전체 반응 차수
*주의 사항
역반응 무시 가능한 반응 초기 등 가정해야 한다
k, n, m은 실험적으로 결정하며 반응식만으로 알 수 없다
k(속도상수)는 반응식의 계수와 비례한다
미분 속도법칙 예시
<미분 속도법칙>
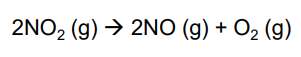
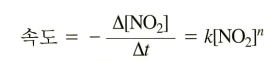
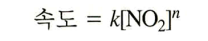
이 때 n은 실험적으로 결정한다. 반응식 계수인 2와는 무관하다
<k와 반응식 계수의 관계>

*반응차수(n)의 결정 - 초기속도법


농도가 반응속도에 0차/1차/2차적으로 영향을 준다
반응차수는 이처럼 계수와 무관, 실험적으로 결정
초기속도법
미분 속도법칙에서, 반응의 유형(=반응식)을 구하는 방법
반응물 농도를 달리하며 초기 속도를 측정한다
실험적으로 반응차수 n, m ..를 결정해야 한다
(1) 반응물 농도 몇 배, 초기 속도 몇 배 비교 → 반응차수 n,m 구함
(2) 아직 k는 모르지만 속도법칙식을 세움 v=k[A]^n[B]^m
(3) (초기농도, 초기속도) 대입 → 반응상수 k 구함
(적분)속도 법칙 : 농도-시간 관계
*정의
한 종류의 반응물만 존재할 경우 ex. 2C4H6(g) → C8H12(g)
반응차수에 따라 식이 달라진다
| 0차 속도법칙 ex. 미분법칙에서 v=k 경우 |
1차 속도법칙 ex. 미분법칙에서 v=k[A] 경우 |
2차 속도법칙 ex. 미분법칙에서 v=k[A]^2 경우 |
| [A]=-kt + [A]0 [A]와 t 그 때의 기울기가 -k   |
ln[A] = -kt + ln[A]0 ln[A]와 t 그 때의 기울기가 -k   |
1/[A] = kt + 1/[A]0 -1/[A]와 t 그 때의 기울기가 -k   |
[A]0/2k |
ln2/k 반감기가 농도에 무관함 항상 일정한 반감기!    |
1/k[A]0 반감기가 초기농도에 반비례! 즉, 다음 반감기는 농도가 1/2이니 반감기는 2배가 된다!  |
| ex. 백금 표면 위에서 일어나는 반응 표면이 반응 분자수를 제한 →계속 일정한 수의 분자만 반응 →속도가 일정함  |

1차 예시
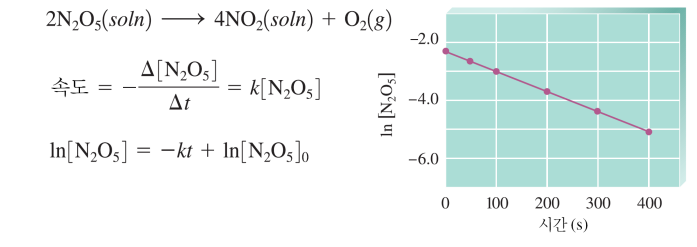
2차 예시
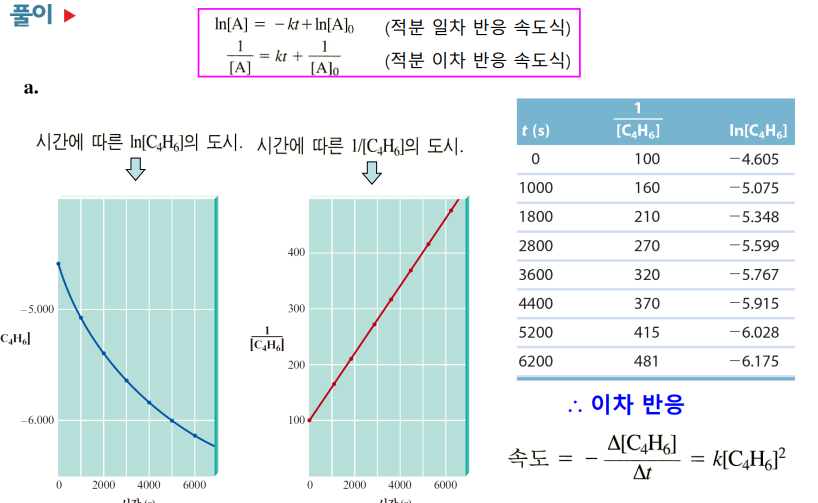
0차 예시
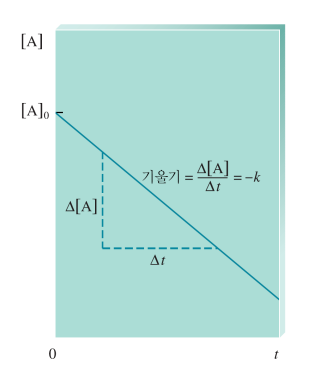
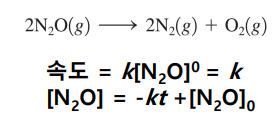
*반응차수(n)의 결정 (식 유형 고르기)
*식 구하기 (k 구하기)
*해당시간의 농도 계산하기
*반감기 구하기
(1) [A], ln[A], -1/[A] 중 선형적인 것 고르기 ▷ 차수 판별
(2) 그래프의 기울기 구해 k 구하기 ▷ k 구하기
(3) 차수에 맞는 식을 골라, k와 [A]0 이용해 식을 세우기 ▷적분속도식 완성
(4) t를 대입해 농도 예측 가능 ▷농도의 계산
(4) 차수에 맞는 반감기 식으로 반감기 구하기 ▷반감기 구하기
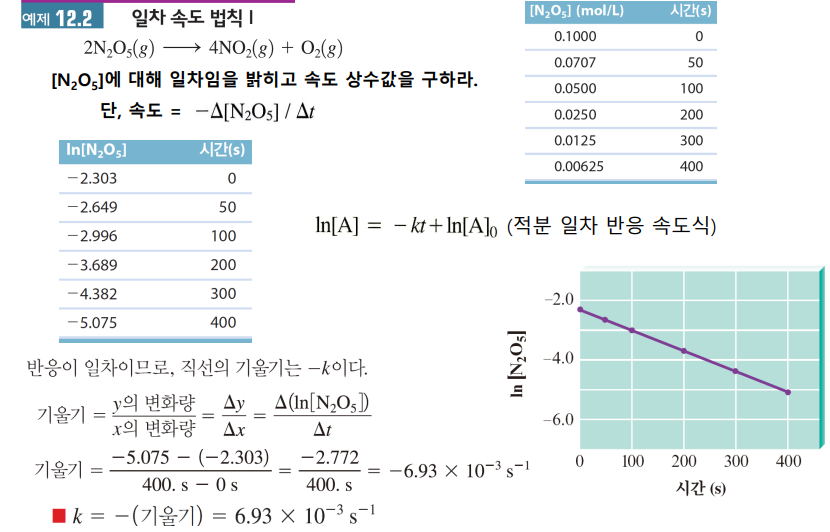
1차 속도법칙 예제
1차 속도법칙
시간-농도 보고 적분속도식 구하기 (k 구하기)
(1) ln[A]가 직선의 기울기를 가짐을 보인다
(2) 그 때의 기울기(-k)를 구한다
(3) k, ln[A]0을 아니 적분 속도식을 세운다
시간-농도 보고 > 적분 속도식 구한 다음 > 특정 시간이 흐른 뒤 농도 예측하기 (농도 계산)

반감기 응용 > 반감기가 주어지면> k를 구하고> 1/4 반감기 구하기
(1) ln2/k=반감기 이용해 k 구하기
(2) ln[A]에 ln[A]*(1/4) 대입하기

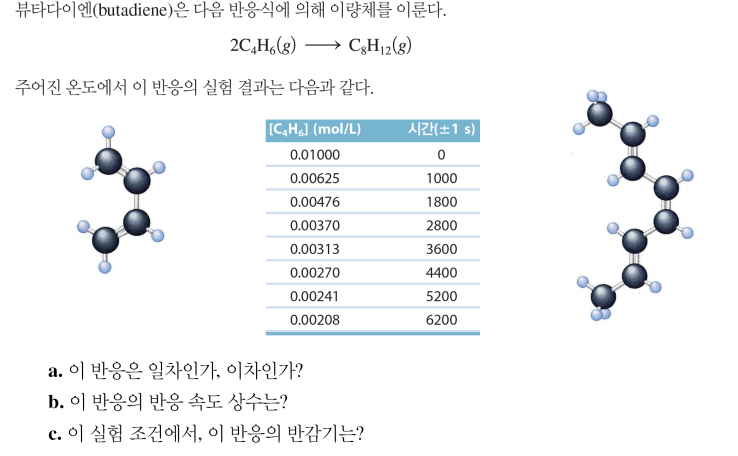
2차 속도법칙 예제
시간-농도 보고> 1, 2차 중 판별> 속도상수 k 구하기> 반감기 구하기
(1) ln[A], 1/[A]로 도사해보고, 일차적인 것을 고르기 ▷ 차수 판별
(2) !2차의 경우! 1/[A] 그래프의 기울기 구해 k 구하기 ▷ k 구하기
**여기서 대입해서 구하고 싶을 수도 있는데.. 뭐 상관 없긴 하군요
(3) !2차의 경우! k와 [A]0 이용해 식을 세우기 ▷1/[A] = kt + 1/[A]0
(4) !2차의 경우! 반감기 식 1/k[A]0 이용해 반감기 구하기


두 종류 이상의 반응물에서 적분 속도식 ex. A + B + C → 생성물
유사 n차 반응을 이용
[A] <<< [B], [C]면 [A]에만 속도가 의존한다
즉, 가장 농도가 낮은 [A]의 차수만 중요해진다
나머지는 농도가 비교적 일정하게 유지되기 때문이다

유사 n차 반응 적분속도식 예시

반응 메커니즘
반응 속도를 알면 메커니즘을 규명할 수 있다
단일 단계 반응, 속도 결정 단계
한 반응은 단일 단계 반응들로 구성된다
중간체는 진행 중 생성되었다 사라지는 화학종이다. 반응물도 생성물도 X
속도 결정 단계란?
가장 느린 단계가 속도를 결정한다
그 때의 계수가 반응차수를 결정한다





(1) 단일 단계 반응을 모두 더하면 전체 반응식이 됨
(2) 반응 메커니즘은 실험적으로 구한 속도 법칙을 만족함
예제
반응 속도론 모형 - 속도 영향 요인
충돌 모형
분자가 충돌해서 반응이 일어난다
| 온도 | 활성화 에너지 | 분자 배향 |
| 온도가 증가 → 분자 운동속도 증가 → 충돌수 증가 → 반응 속도 증가  속도 상수가 증가한다 |
화학 반응을 진행하기 위한 최소한의 문턱 에너지 전이 상태: 퍼텐셜 에너지의 정점  충돌 에너지가 활성화 에너지보다 커야만 반응이 일어남 <유효 충돌> (충돌 전의 운동에너지가.. 결합을 끊고 퍼텐셜 에너지로 변화?!)  |
적절한 분자배향일 때만 충돌했을 때 반응이 일어남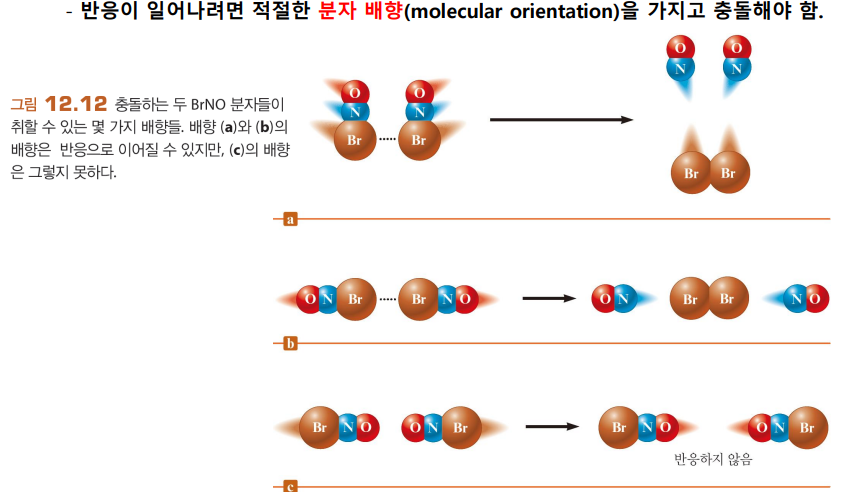 |
| ex. 냉장고에서는 부패가 잘 안 일어남 ex. 높은 온도에서만 연소 |
Q. 그럼 온도는 충돌수로 한 번(빈도의 증가..), 활성화 에너지로 한 번(비율의 증가..) 총 두 번 영향을 주는 거임??
Q. 운동 에너지가 퍼텐셜 에너지로 변한다라.. 근데 에너지가 높아지면 안 좋은 거 아님?? 그럴 수 있나..?? 머지.. 헤헤..
그리고 결합이 끊기면.. 에너지가 소요되는데.. 그건 생각해보면.. 어디로 가는 거지.. 내가 뭘 감을 못 잡고 있는 지도 모르겠다... 에너지는 보존 되자나... 결합을 끊기 위해... 끊었어.. 그럼 불안정해지나...? 그러면 퍼텐셜 에너지로 바뀌는..?
그러면 분자가 작은 에너지를 가지게 되어서 결합을 한다는 것은... 뭐지... 결합해서 안정해짐.. 그럼 에너지가 방출 될 거고.. 그 에너지는 어디로 가지.. 열? 그래서 발열 반응? 그래서 열이 나서 온도가 높아지면... 또 다른 애가 운동 에너지가 높아지는 건가...? 그 운동에너지를 받아서.. 유효충돌을 해서 반응을 하게 되나..?? 아 뭔가 혼란스럽다..^^ 겁나 루미큐브 하는 것 같아;;
Arrhenius 식




k = zpe^(-Ea/RT)
k는 반응 속도 상수
z:충돌 횟수 p:유효배향충돌분율(입체인자) zp=A;잦음률
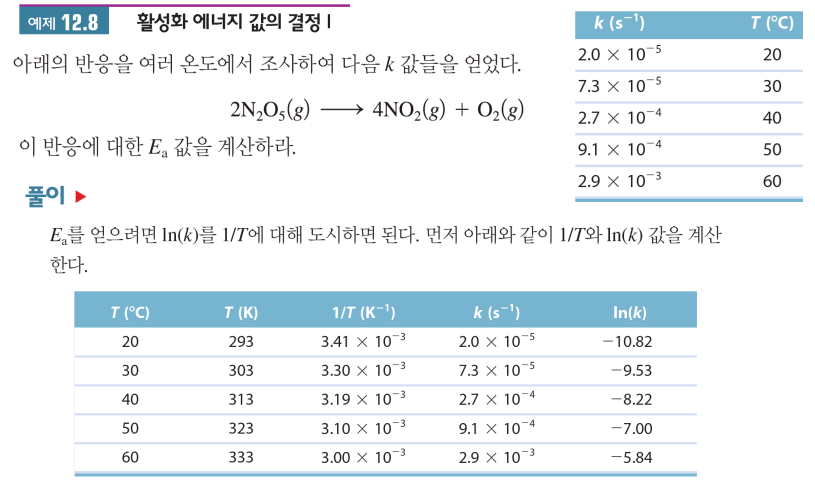
* 아레니우스 식 응용: 온도-반응상수 보고 활성화 에너지 구하기
(1) lnk, 1/T에 대한 일차함수 구하기
(2) 기울기가 -Ea/R이니 Ea 구할 수 있음
** 에너지의 단위는 J/mol
** R=8.3145J/(K*mol)
예제1
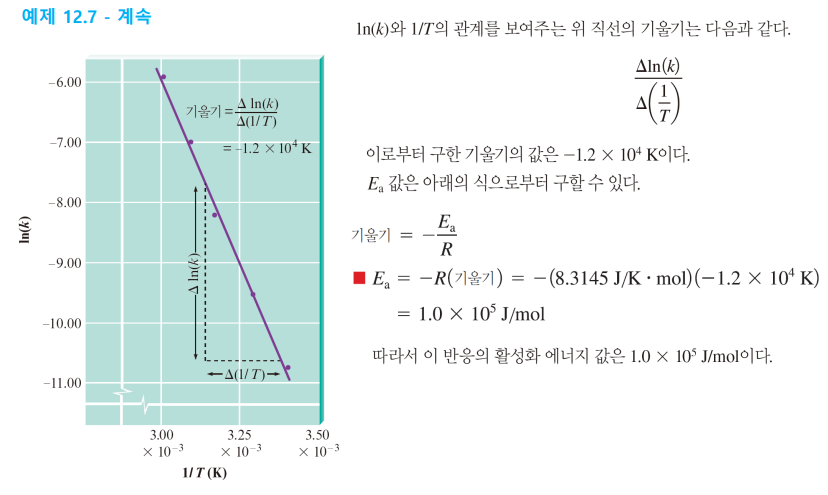
예제2

촉매
낮은 활성화 에너지의 새로운 경로를 뚫어줌
→ 유효 충돌 기준이 완화됨
→ 동일 온도 조건에서 유효 충돌 분율이 증가
→ 반응 속도 증가
온도를 높이지 않아도 반응 속도 증가하니, 생체에서 유용



| 균일 촉매 -반응물과 같은 상 |
불균일 촉매 -반응물과 다른 상(고체) |
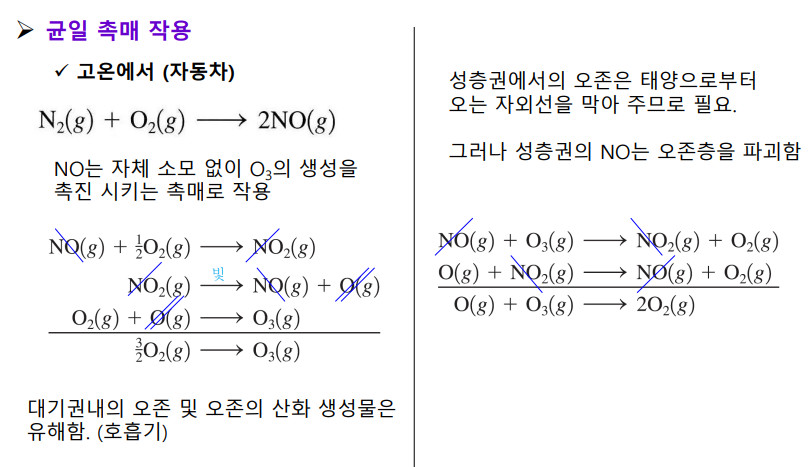 |
흡착 ex. 백금 촉매  |
더 공부할 것
R과 에너지의 관계 복습하기..
J 등 단위 복습
'일반화학 > 일반화학 개념정리' 카테고리의 다른 글
| <일반 화학> 14장- 산과 염기 (1) | 2023.09.18 |
|---|---|
| <일반 화학> 13장- 화학 평형 (0) | 2023.09.11 |
| <일반 화학> 11장- 용액의 특성 (0) | 2023.05.30 |
| <일반 화학> 10장- 액체와 고체 (1) | 2023.05.24 |
| <일반 화학> 8장 후반~9장- 공유 결합: 오비탈 (1) | 2023.05.19 |









댓글